A triangle with rounded corners in C#

For one of my projects I needed to draw triangles with rounded egdes, and since I didn’t found anything about this topic elsewhere, I had to figure it out by myself. Luckily no mathematics is needed, except the Pythagorean theorem. So here’S how I did it, complete with a sample implementation using C#.

To make things easier, I started with a right-angled triangle where the two sides forming the right angle are vertical and horizontal. This makes applying a rounded corner for the right angle easy, since it is a common problem known from drawing rounded rectangles. You’ll find examples for this all over the net. I instead will discuss, how to round the two other edges, which both form an angle of 45 degrees.

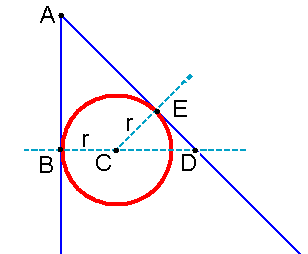
Here’s a sketch demonstrating the problem. A circle with radius r needs to be placed at point C for the two sides forming the triangle becoming its tangents. How do we calculate C? Well, we already know that the length of BC is r, so we just need to figure out the length of AB. AB itself has the same length then BD, whitch is the sum of BC and CD, where BC is r:

AB = BD
AB = BC + CD
AB = r + CD

Now the points C, D, and E form another right-angled triangle with CE = ED = r. So we can apply the Pythagorean theorem:

AB = r + CD
AB = r + sqr(CE * CE + ED * ED)
AB = r + sqr(r * r + r * r)
AB = r + sqr(2 * r * r)
AB = r + sqr(2) * r
AB = (1 + sqr(2)) * r

For drawing circles or parts of it in C#, we need to provide the surrounding rectangle R, which obviously starts at Rx = Cx - r and Ry = Cy - r.

Rx = Cx - r = Ax
Ry = Cy - r = Ay + (1 + sqr(2)) * r - r
Ry = Ay + (1 - 1 + sqr(2)) * r
Ry = Ay + sqr(2) * r

Here’s the C# code to contruct a rounded rectangle’s graphic path. The right angle is rounded with double radius, just because it looks better:

// Build it in default size, pointing to left bottom,

// so 90° angle is left bottom.

int radius = 10;
int widthArcRect = 2 * radius;
int left = 0;
int right = 100;
int bottom = right;
int top = 0;
int cornerDist = (int)(Math.Sqrt(2) * radius);
GraphicsPath p = new GraphicsPath();
// bottom left corner (90°)

p.AddArc(left, bottom - 2 * widthArcRect, 2 * widthArcRect, 2 * widthArcRect, 90, 90);
// left line

p.AddLine(left, bottom - 2 * widthArcRect, left, top + cornerDist + widthArcRect);
// top corner

p.AddArc(left, top + cornerDist, widthArcRect, widthArcRect, 180, 135);
// diagonal line

p.AddLine(left + cornerDist, top + cornerDist, right - cornerDist, bottom - cornerDist);
// right corner

p.AddArc(right - cornerDist - widthArcRect, bottom - widthArcRect, widthArcRect, widthArcRect, 315, 135);
// Bottom line

p.AddLine(right - cornerDist - widthArcRect, bottom, left + 2 * widthArcRect, bottom);
p.CloseFigure();

Now having the triangle, we can transform it, to point in any directions and to have any size. If for example we want to draw a triangle pointing to the right beeing 20 pixel in height, we apply the following transformation:

int newHeight = 20;
Matrix m = new Matrix();
// Rotate

PointF center = new PointF((right - left)/ 2, (bottom - top) /2 );
m.RotateAt(-135, center);
// Rotated triangle is larger than the original

int widthOriginal = (right - left);
float lengthHypotenuse = float(Math.Sqrt(2) * width);
m.Translate(- width / 2, (lengthHypotenuse - width) / 2);
// Scale to fit size

float scale = (float)(newSize / lengthHypotenuse);
m.Scale(scale, scale);
// Apply Matrix

p.Transform(m);

What is happening here? After rotating, the triangle’s bounding rectangle is higher then the original, since the hypotenuse is now vertical. The length of the hypotenuse (Lh) is:

Lh = sqr(width * width + width * width)
Lh = sqr(2 * width * width)
Lh = sqr(2) * width;</code>

We now have to move the triangle down a bit, so that its top corner is within the orignals path boundaries (This makes positioning much easier). The amount we have to move is the lengh of the hypotenuse minus the width divided by two. We also have to move the whole triangle to the left, since it was rotated at its bounding rectangle’s center, which now forms the left side of the triangle. Afterwards the triangle is scaled, since we want the hypotenuse to be 20 pixel in height.

After the transformation, we have a right angled triangle with rounded edges, pointing to the right, and 20 pixel in height. We now can apply a last transformation to place it at the coordinates (5, 10), for example:

m.Translate(5, 10);